Fictos Developer Tools

Plot Area Calculator

Area Calculator for 4 sided plots

rectangle area

To determine the area of a rectangle, you can ascertain it by multiplying the length of one side by the length of another side, perpendicular to the first:

Area = Length of Side A * Length of Side B






Quadrilateral Area Calculator with Diagonal

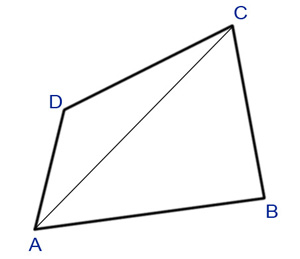
irregular rectangle / plot

Here's an alternative explanation for calculating the area of a quadrilateral by splitting it into two triangles and using Heron's formula: When dealing with a four-sided plot, whether regular or irregular, you can partition it into two triangles. The area of each triangle can then be computed using Heron's formula, which accounts for all three side lengths:

Area of a Triangle = √[s(s - a)(s - b)(s - c)]









Atleast one diagonal is required





Irregular / Trianle / Polygon / Uneven Rectangle / Trapezoid Area Calculator

Choose the number of sides (3 to 10) and enter the lengths of each side.

Results

Length Converter

Area Converter

FAQ

The tool supports polygons with a minimum of 3 sides and a maximum of 10 sides.

For polygons with 3 sides, Heron's Formula is used. For quadrilaterals, Bretschneider's Formula is applied. For polygons with 5 to 10 sides, Shoelace Theorem (Gauss's Area Formula) is used.

Yes, the tool allows you to input side lengths in meters, feet, inches, centimeters, yards, kilometers, and miles. The result is displayed in multiple units, including square meters, feet, yards, centimeters, cents, and acres.

Messages

Note: Please ensure that the side lengths are valid for the polygon you are trying to calculate.

Error: The side lengths provided cannot form a valid polygon. Please check the input values and try again.

Success: The area has been calculated successfully!

Length Conversion

  • 1 yard (yd) ≈ 3 feet (ft)
  • 1 foot (ft) ≈ 12 inches (in) ≈ 30.48 centimeters (cm)
  • 1 inch (in) ≈ 2.54 centimeters (cm)
  • 1 meter (m) ≈ 100 centimeters (cm) ≈ 39.37 inches (in) ≈ 3.28 feet (ft)
  • 1 kilometer (km) ≈ 1000 meters (m) ≈ 0.621 miles (mi)
  • 1 mile (mi) ≈ 1.609 kilometers (km)

Area Conversion

  • 1 square foot (ft²) ≈ 0.09 square meters (m²)
  • 1 square meter (m²) ≈ 10.76 square feet (ft²)
  • 1 square yard (yd²) ≈ 9 square feet (ft²)
  • 1 cent (c) ≈ 435.61 square feet (ft²) ≈ 40.46 square meters (m²)
  • 1 are ≈ 100 square meters (m²)
  • 1 acre ≈ 100 cents ≈ 4046.86 square meters (m²)
  • 1 hectare ≈ 2.47 acres ≈ 100 ares ≈ 10,000 square meters (m²)
  • 1 bigha ≈ 20 katha ≈ 13,068 square feet (ft²) (may vary by region)
  • 1 katha ≈ 720 square feet (ft²) (may vary by region)
  • 1 gaj ≈ 9 square feet (ft²)
  • 1 guntha ≈ 1089 square feet (ft²) ≈ 101.17 square meters (m²)